Convection in a Fluid Loop

Abstract

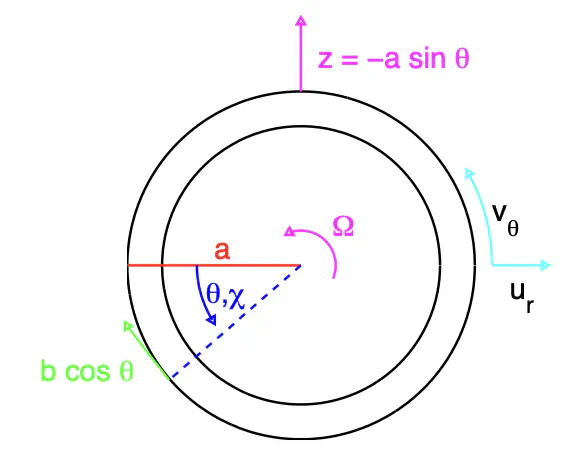
Sandström’s conjecture states that a closed steady circulation can only be maintained in a fluid body if the heating is applied at a lower level than the cooling. In the ocean this has been taken to mean that there can not be a purely buoyancy-driven circulation since the primary sources of heat and salt are applied at the surface. Using the one-dimensional fluid loop of Welander with boundary condition of temperature relaxing to warm and cold at the same geopotential, we find that Sandström’s conjecture holds; circulation and horizontal heat transport all vanish as the Rayleigh number R −→ ∞ (the limit relevant for the ocean). However, if we specify fixed temperature flux boundary conditions, then contrary to Sandström’s conjecture, circulation does not vanish as R −→ ∞. Thus Sandstro ̈m’s conjecture is sensitive to the particular choice of boundary conditions specified. In the case of the ocean, where salinity and sensible heat also play a role in forcing the system, it is not clear that fixed temperature rather than fixed flux boundary conditions at the surface are appropriate. This system of horizontal convection in a loop is stable, but becomes chaotic as the heat sources are rotated from horizontal to vertical positions (heating at the bottom and cooling at the top). We determine the orientation of the heating and cooling at which this transition to chaos occurs. We also show how the strength of the circulation responds to different positioning of heating and cooling.